Poincare half plane
It is a model for the axiomatic hyperbolic geometry.
It consists of the upper half complex plane
$$ \mathbb{H}=\{x+yi : y>0\} $$together with the metric
$$ d\hat{s}=\frac{ds}{y}, $$or, in other words,
$$ g = \begin{pmatrix} \frac{1}{y^2} & 0 \\ 0 & \frac{1}{y^2} \end{pmatrix}. $$A subgroup of the Moebius transformations of the Riemann sphere acts on $\mathbb H$.
There is a conformal map from the pseudosphere to $(\mathbb H,g)$.
What about their geodesics? Since this is a conformal map (in the usual sense of the word "map") the metric can be seen like this
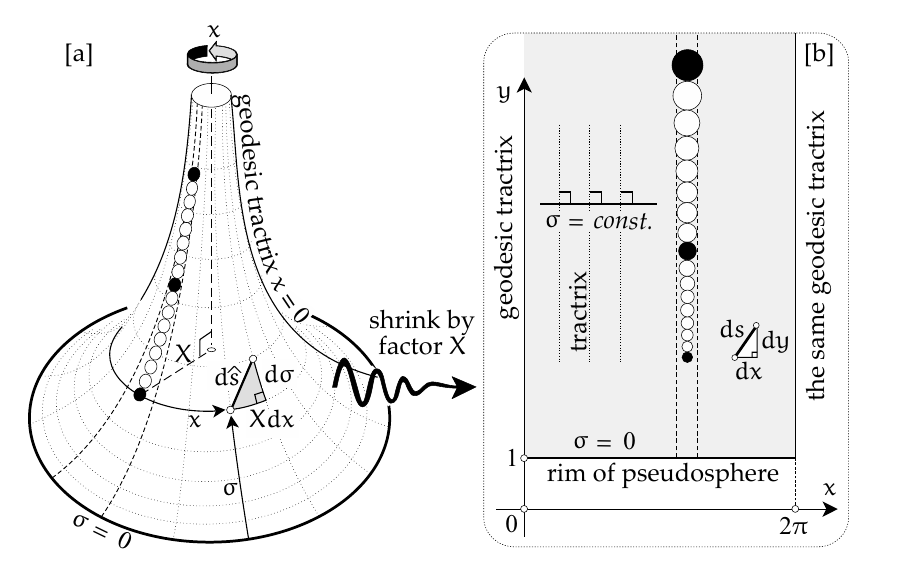
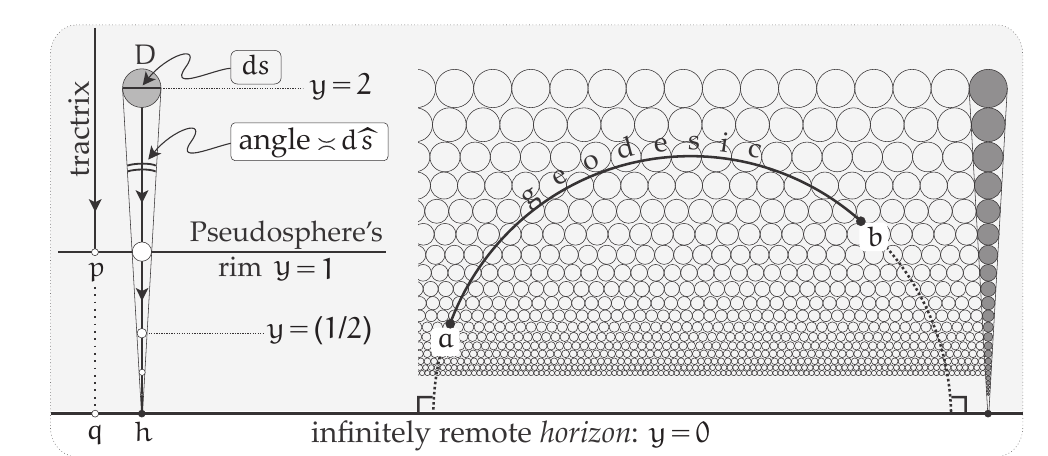
See @needham2021visual page 55-57 for details. Every little circle in the map represent a unit of length in the pseudosphere. The conformal requirement is for the circles not to be ellipses. With this picture in mind, geodesics will be lines which go through the fewest amount of circles.
It is related to Snell law for the relation between the angles of light going through two different materials.
Infinite parallels
See @needham2021visual page 61:

Map to the Poincare disk
Define the complex coordinate $z=x+iy\in \mathbb{H}$, and define the new complex coordinate $u$ by the relation $$iu = \frac{1+iz}{1-iz} \qquad \Leftrightarrow \qquad iz = \frac{-1+iu}{1+iu} \, . $$ It is easy to check that this establishes a bijection between $\mathbb{H}$ parametrized by $z$ and the Poincaré disk $$\mathbb{D} = \{ u \in \mathbb{C} \mid |u|<1 \} \, . $$ The metric on the hyperbolic plane and the Poincaré disk in complex coordinates are
$$ g_{\mathbb{H}} = \frac{\mathrm{d} z \mathrm{d} \bar{z}}{(\mathrm{Im} \, z)^2} = \frac{4 \mathrm{d} u \mathrm{d} \bar{u}}{(1-|u|^2)^2} \, . $$One can check that the Ricci scalar is again constant and equal to $R=-2$.
Tridimensional version
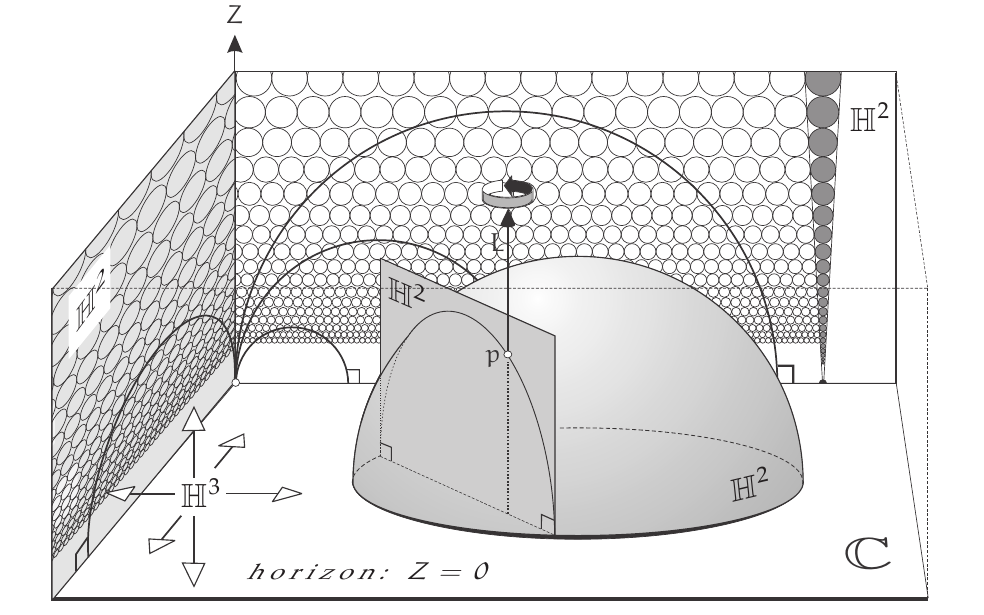
See @needham2021visual page 80.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: